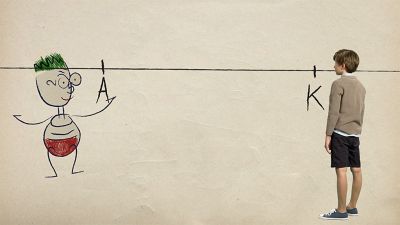
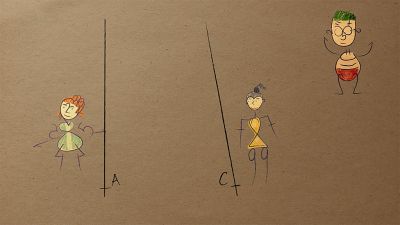
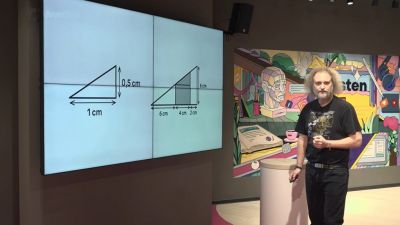
UčíTelka (5. tř.): Úhel

Když děti učí telka! Seznámíme se s žáky 5. ročníku s pojmem úhel. Ukážeme si, jak máme rozeznat a modelovat úhel. Vysvětlíme si, jaké jsou rozdíly mezi úhlem pravým, úhlem ostrým a úhlem tupým.

Z pořadu:

• UčíTelka

Témata:

• Geometrie v rovině

Vhodné pro stupeň:

• 1. stupeň ZŠ

Vhodné pro předmět:

• Matematika

Klíčová slova:

• Veronika Dobrovolná
• pravý úhel
• úhel